5 Axial Loading
Introduction
Click to expand
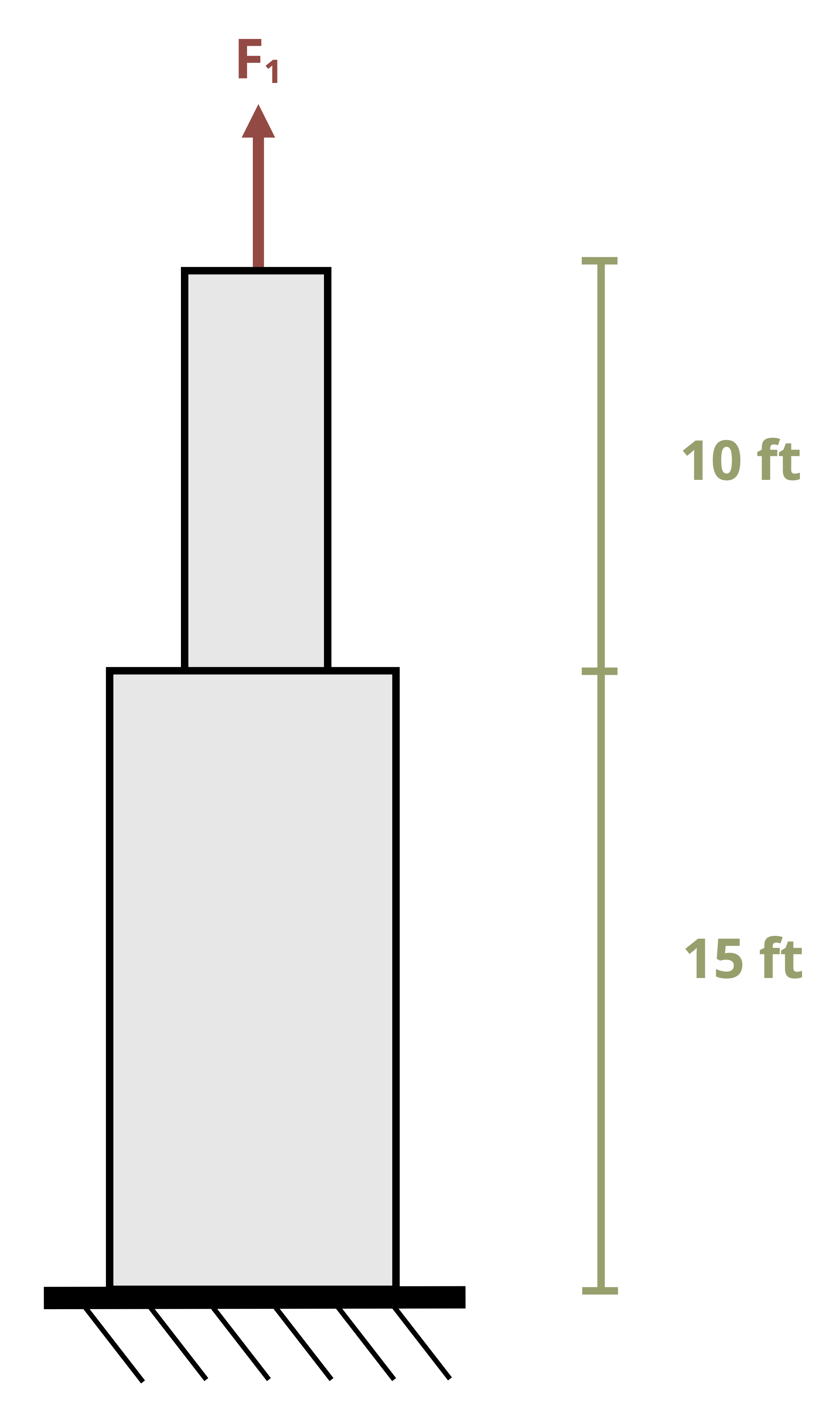
In this chapter we’ll take a closer look at the effects of axial loading. Axial loads are those applied perpendicular to the cross-section of an object (Figure 5.1) and such loads affect the object in several ways.
Axial loads create axial stresses, which we have already seen in Section 2.1 and we’ll revisit briefly in Section 5.1. We previously considered the average normal stress in a cross-section, but the geometry of the cross-section can cause large localized stresses much higher than the average. We’ll discuss these stress concentrations in Section 5.2.
This text is concerned with both stress and deformation, so in Section 5.3 we’ll explore the deformation caused by axial loads. We’ll extend this to a special case of axial deformation involving parallel bars in Section 5.4, before using our knowledge of axial deformation to help us solve statically indeterminate problems in Section 5.5. These are problems where the equilibrium equations are not sufficient to determine the reaction and internal forces.
Finally we’ll investigate the effects of temperature in Section 5.6. As the temperature of an object changes it will expand or contract. Thus there can be deformation even in the absence of any applied forces.
5.1 Axial Stress
Click to expand
Axial loads create axial stresses, also known as normal stresses. As discussed in Section 2.1, the average normal stress is calculated from
\[ \sigma=\frac{N}{A} \]
5.2 Stress Concentrations
Click to expand
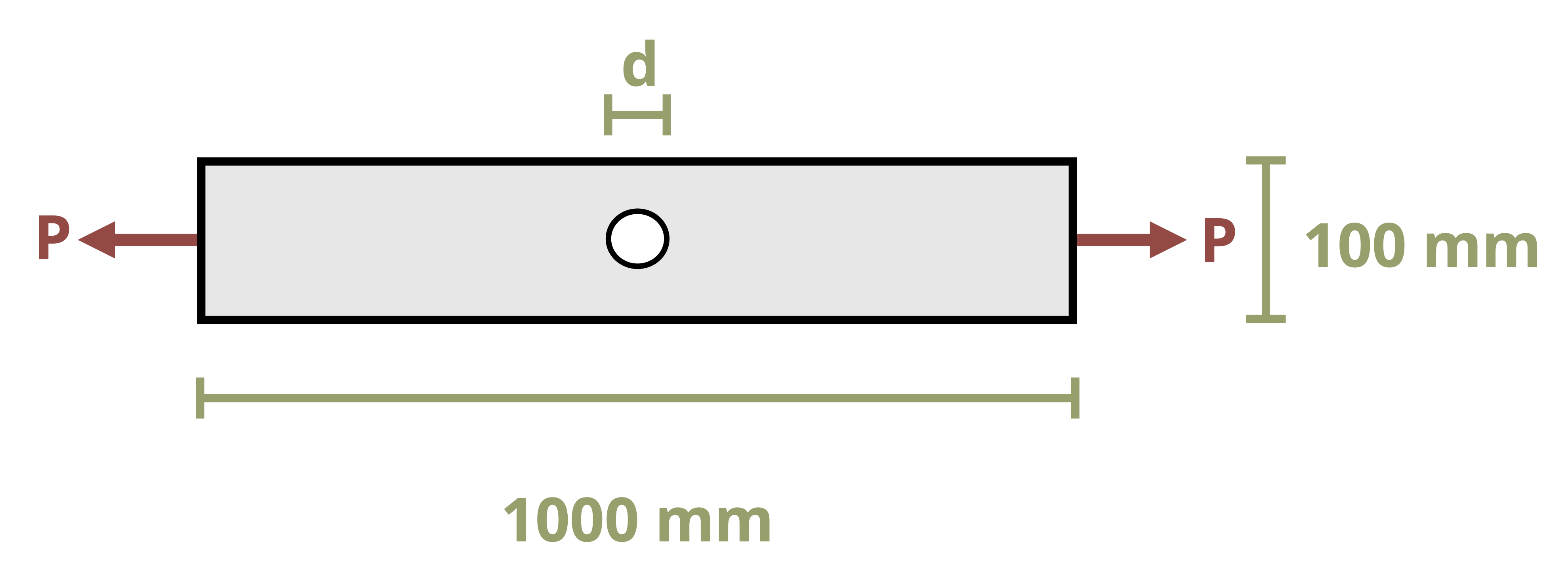
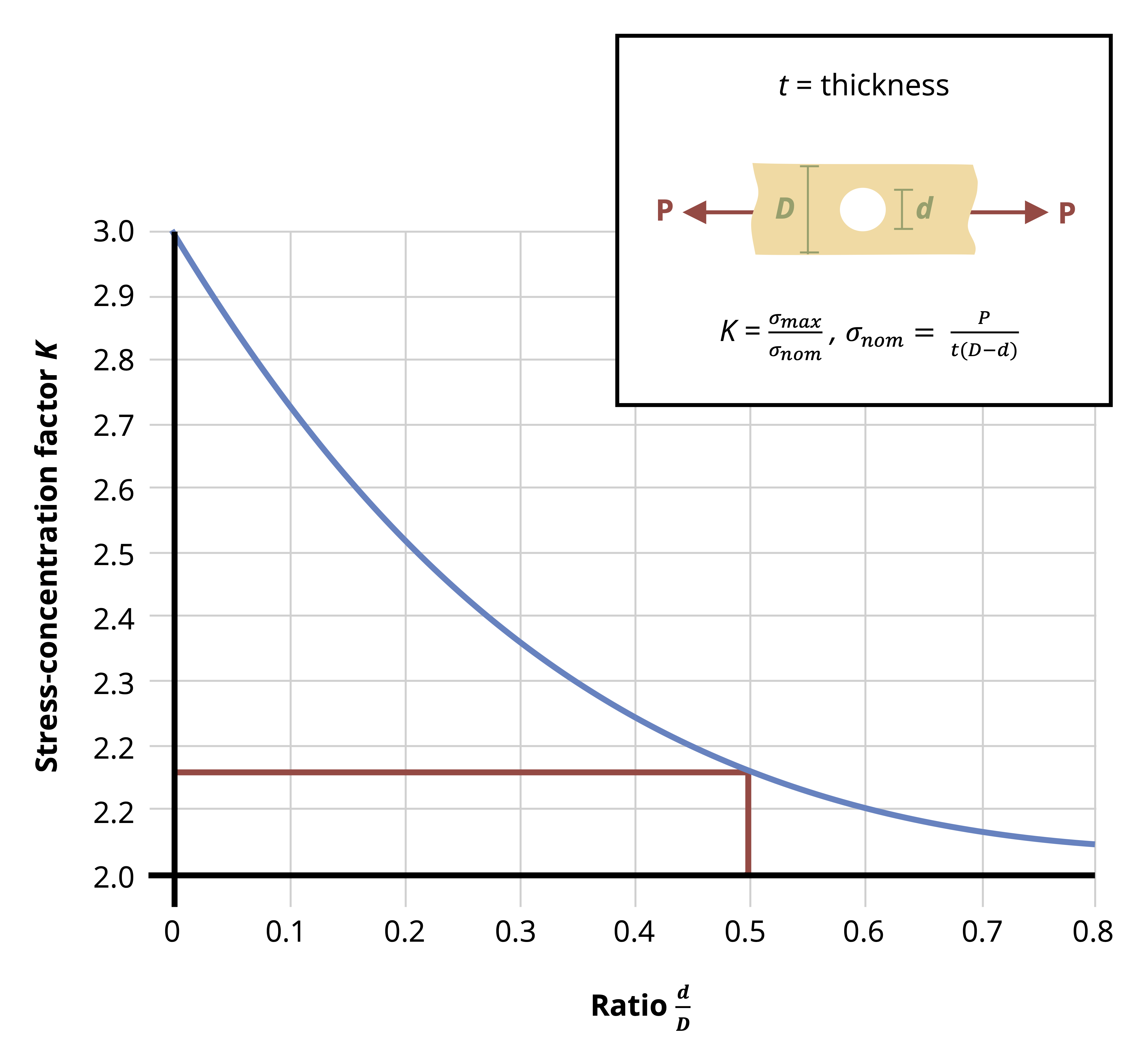
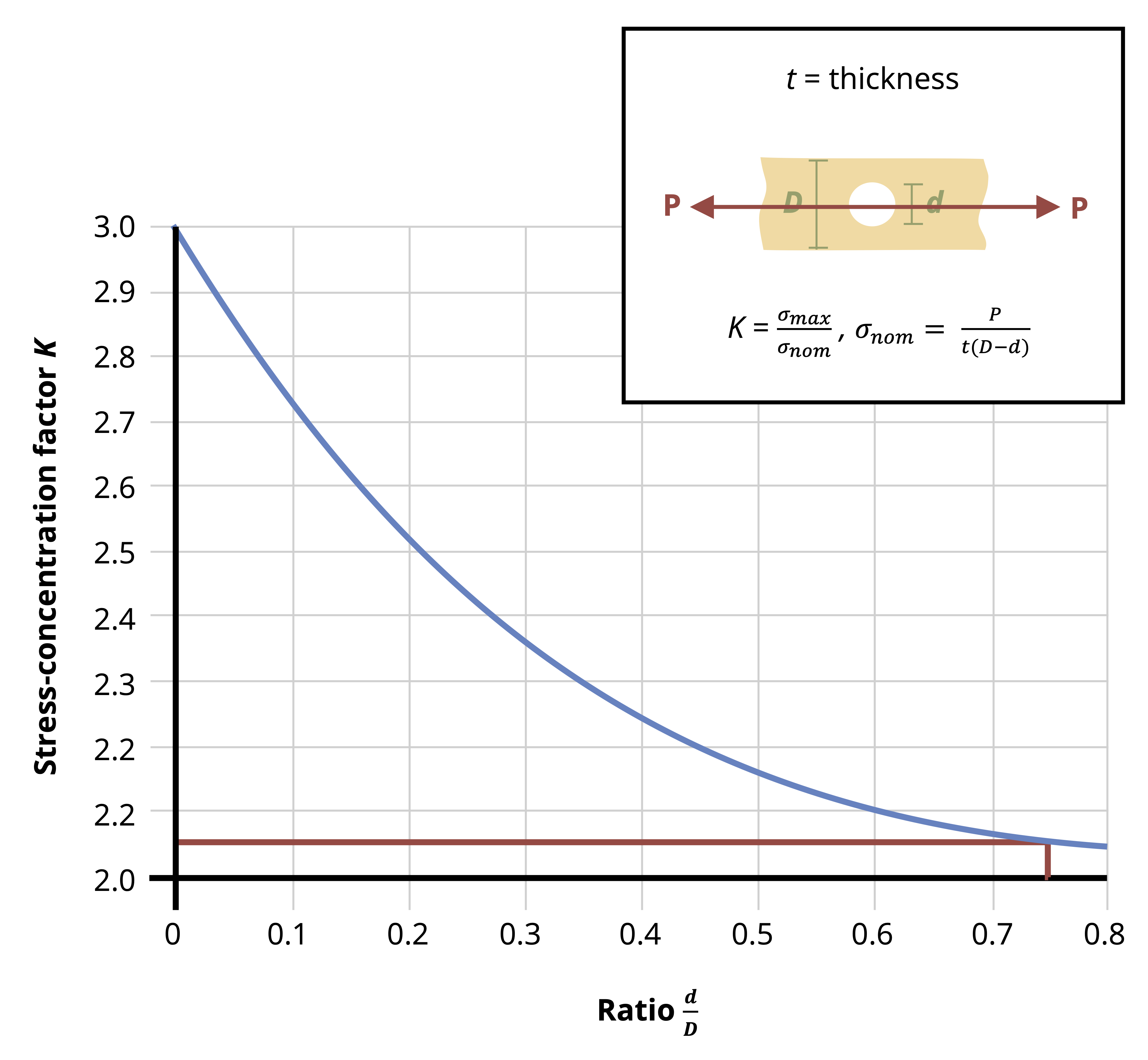
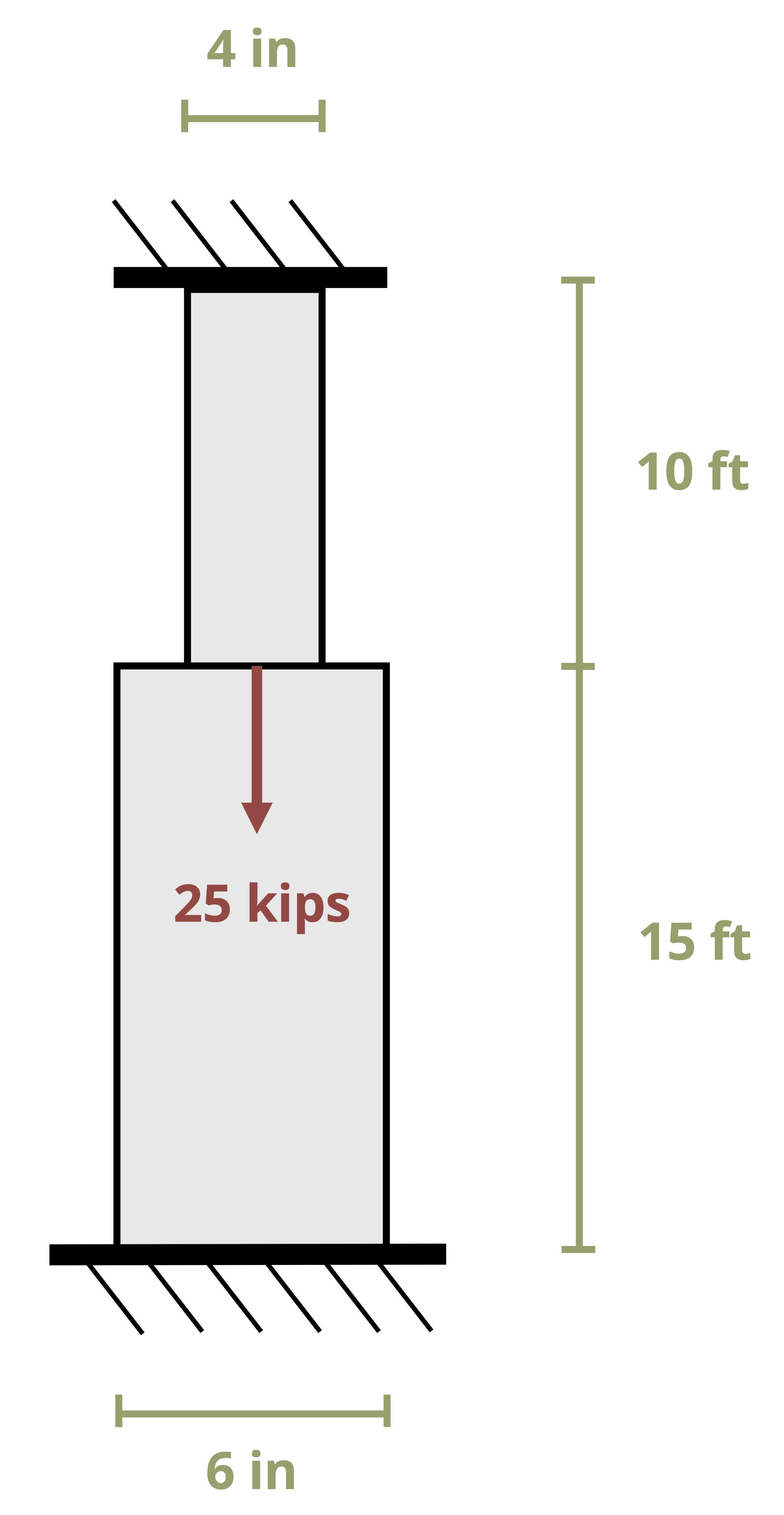
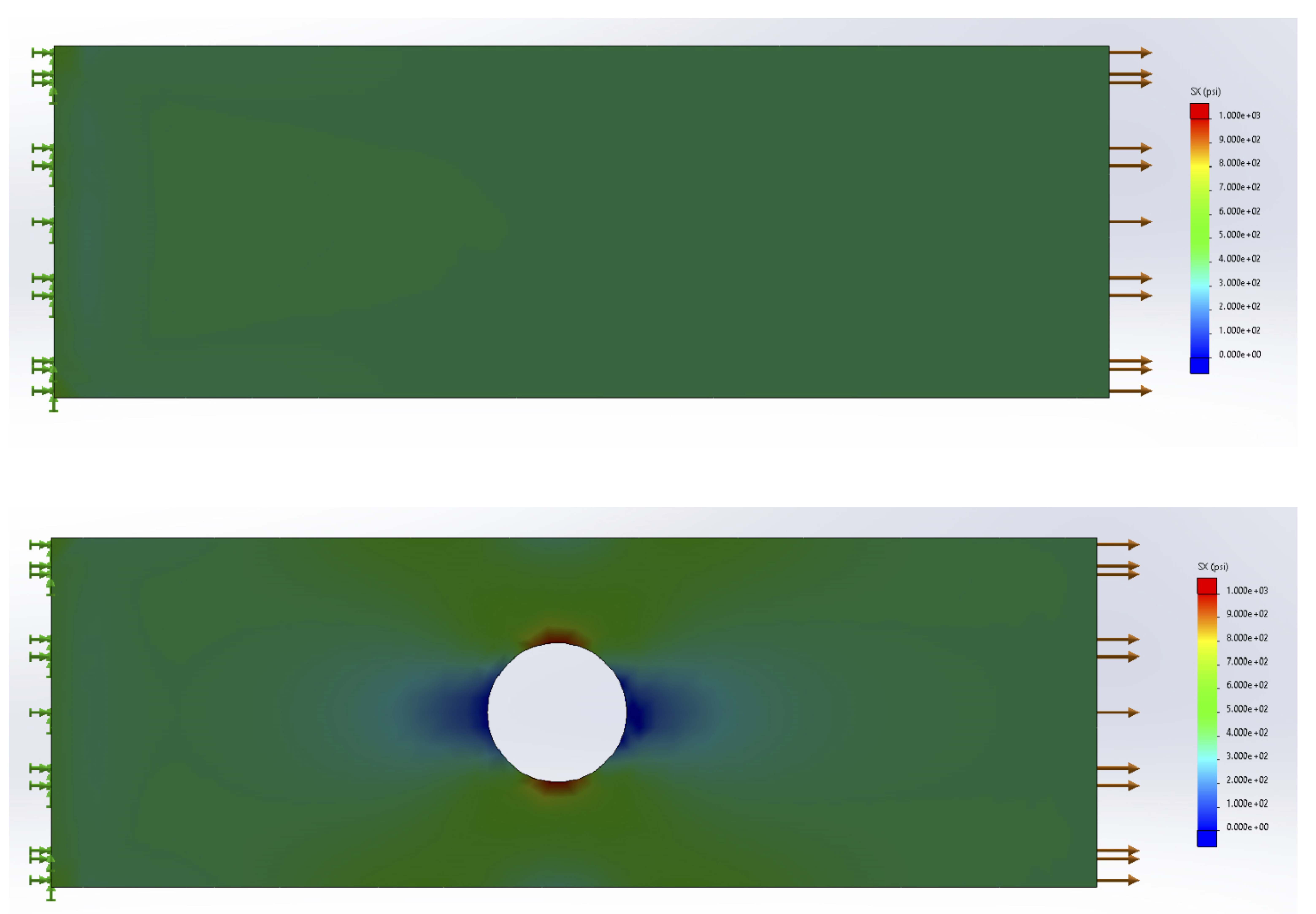
The normal stress discussed in the previous section is averaged over the cross-section and assumes that stresses (and therefore strains) at the cross-section are uniform. In reality stresses and strains can vary across a cross-section, especially if the cross-section is close to an applied load, a support, or a change in geometry. At these points localized stress concentrations occur, leading to large, localized stresses and strains. The intensity of these concentrations depends on the type of loading, support, or geometry (Figure 5.2).
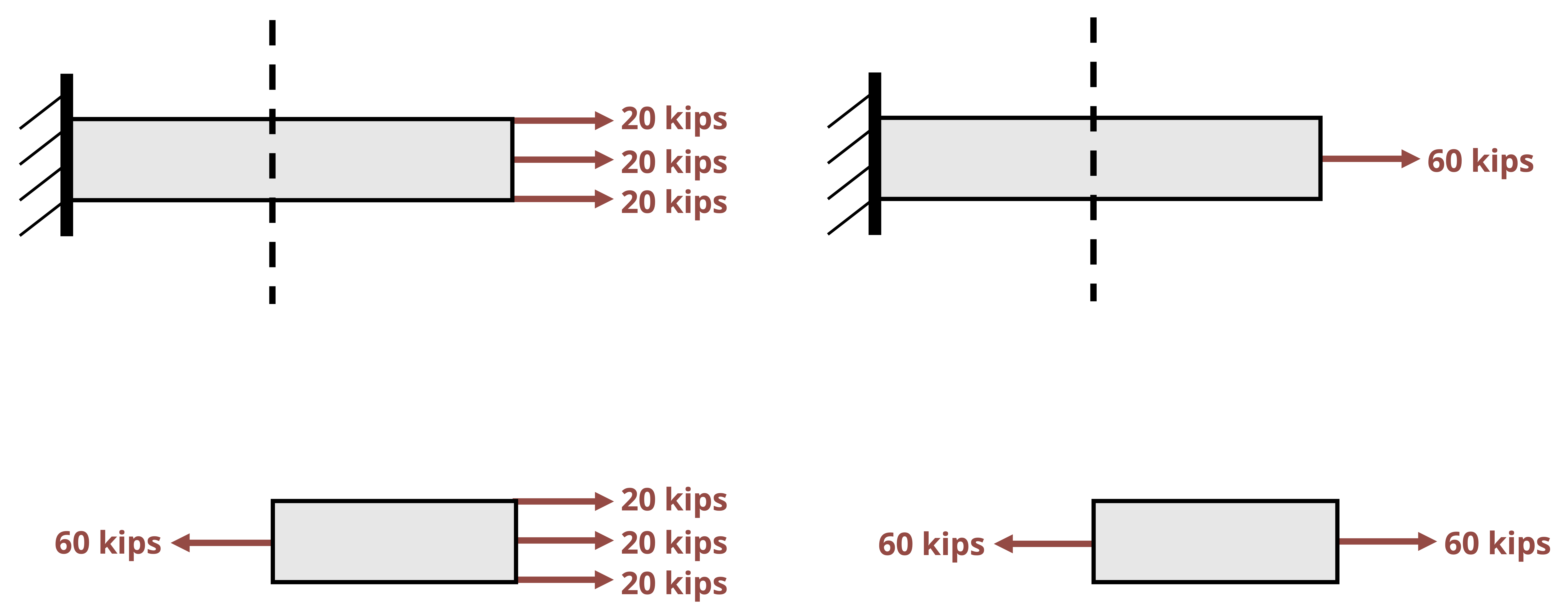
However, these effects disappear a certain distance away from the force, support, or local geometry. It is therefore acceptable to assume uniform stress and strain (as we have been so far) provided that we also assume our cross-section is a sufficient distance away from these points. This is known as Saint-Venant’s principle, which can be formally stated as “The stresses and strains created at a point in a body by two statically equivalent loads are equivalent at points sufficiently far removed from the applied load” (Figure 5.3).
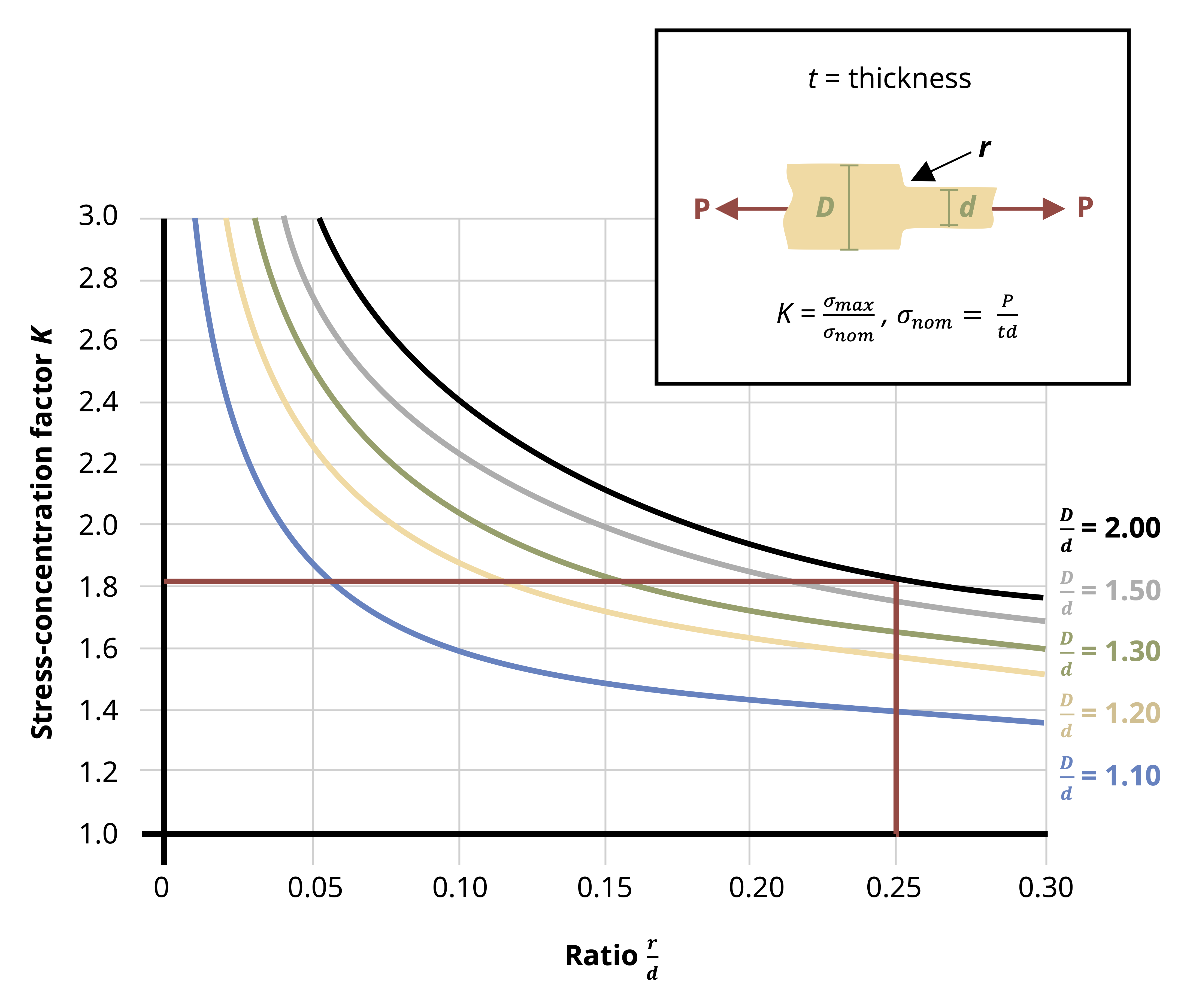
More advanced courses will use the theory of elasticity to study the areas of variable stress and strain, but for now we’ll continue to apply Saint-Venant’s principle and assume that our cross-sections are sufficiently far away from the applied loads that we don’t need to consider these stress concentrations. We will however address the question of stress concentrations around changes in geometry here. We’ll study two specific examples; holes and fillets. Figure 5.2 shows an example of the stress concentrations around a hole. Figure 5.4 shows an example of the stress concentrations around a fillet. A fillet is a rounded corner used to help transition between two geometries.
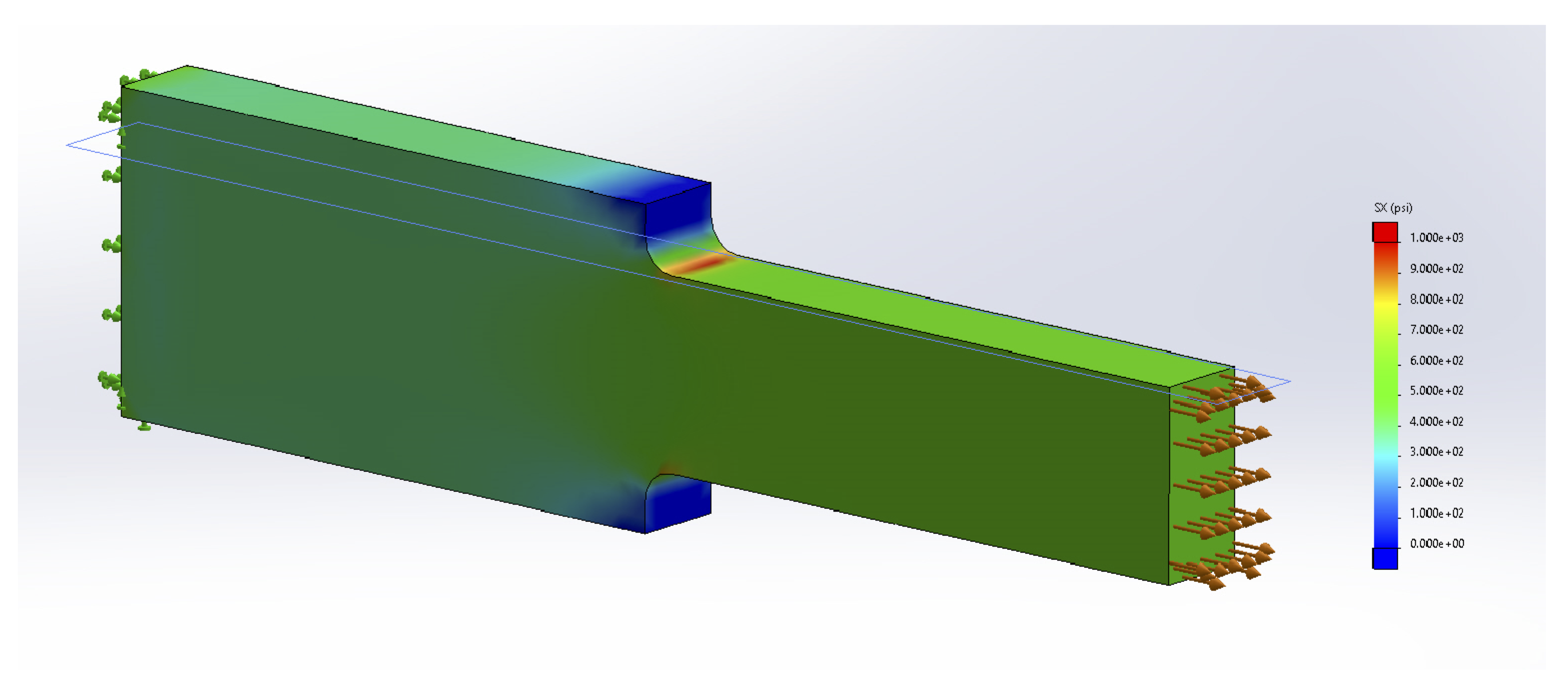
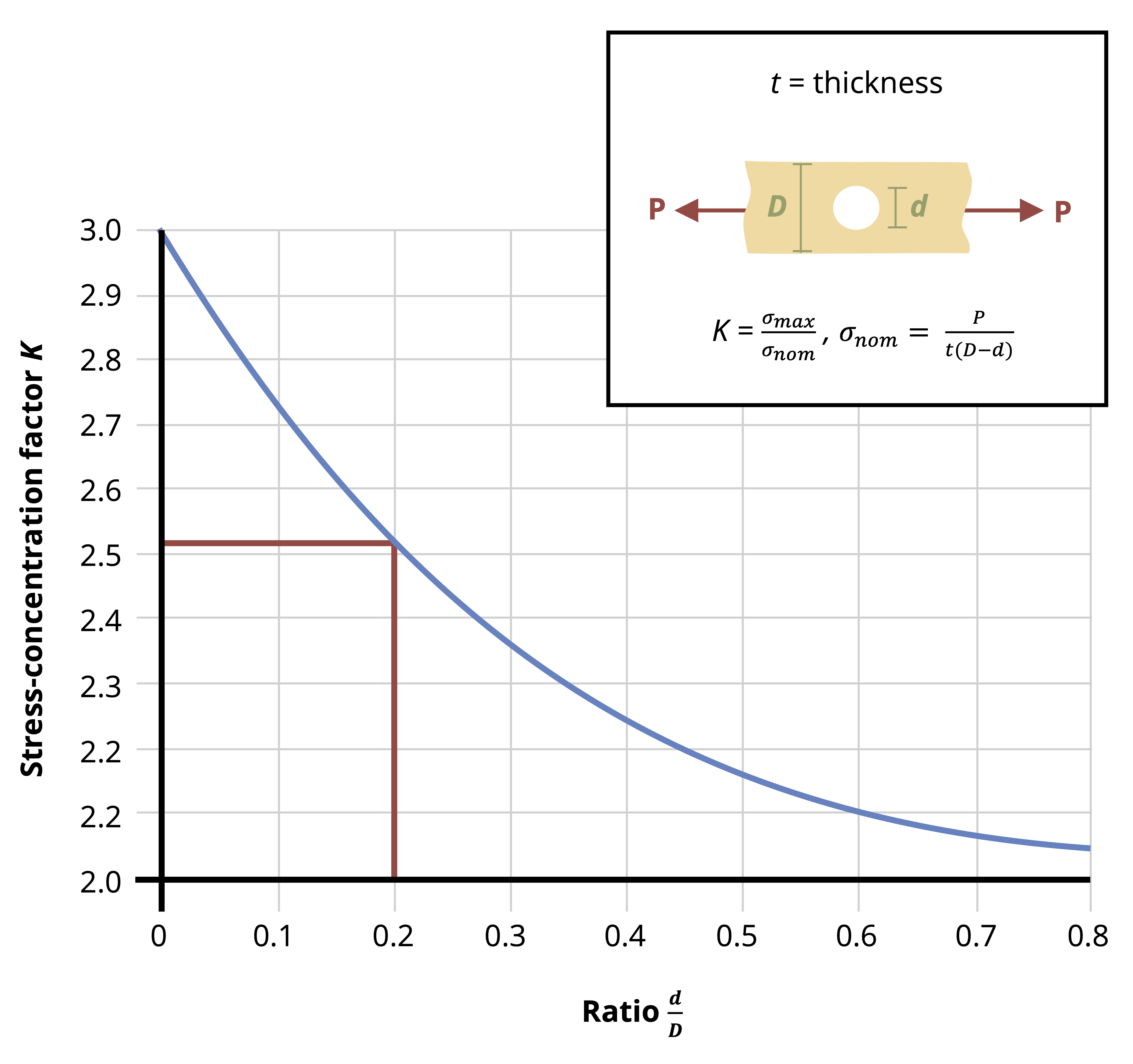
Fully modeling these stress concentrations is very complicated, but for our purposes it is sufficient to find only the maximum stress that occurs around these stress concentrations. These can be significantly larger than the average stress we have been calculating, and can cause localized failure even if the average stress is below the yield stress for the material. The maximum stress can be found simply by multiplying the average stress by a stress concentration factor, K.
\[ \boxed{\sigma_{max}=K \sigma_{avg}} \tag{5.1}\]
𝜎max = Maximum normal stress [Pa, psi]
K = Stress concentrtion factor
𝜎avg = Average normal stress [Pa, psi]
This stress concentration factor depends on the geometry at hand and can be found from curves in design handbooks (Figure 5.5). See Example 5.1 and Example 5.2 to see how these curves can be used.
5.3 Axial Deformation
Click to expand
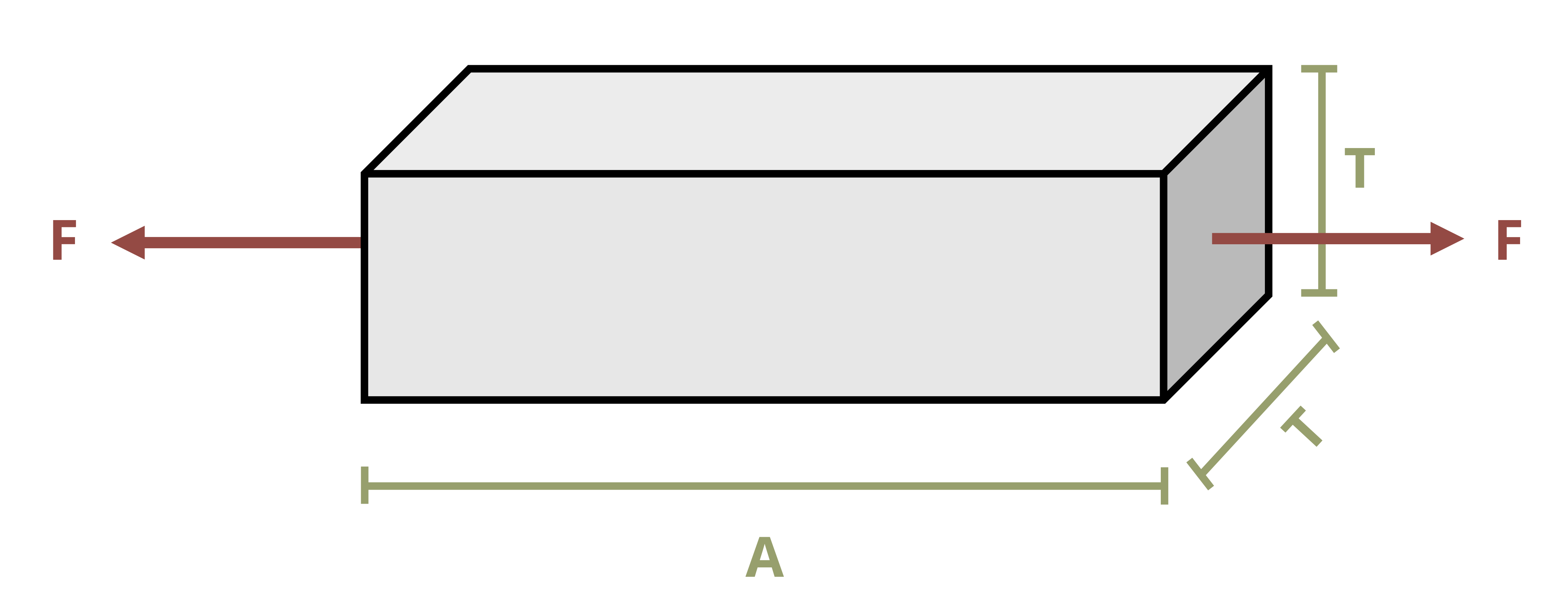
Consider a simple bar of uniform cross-section subjected to an axial force (Figure 5.6).
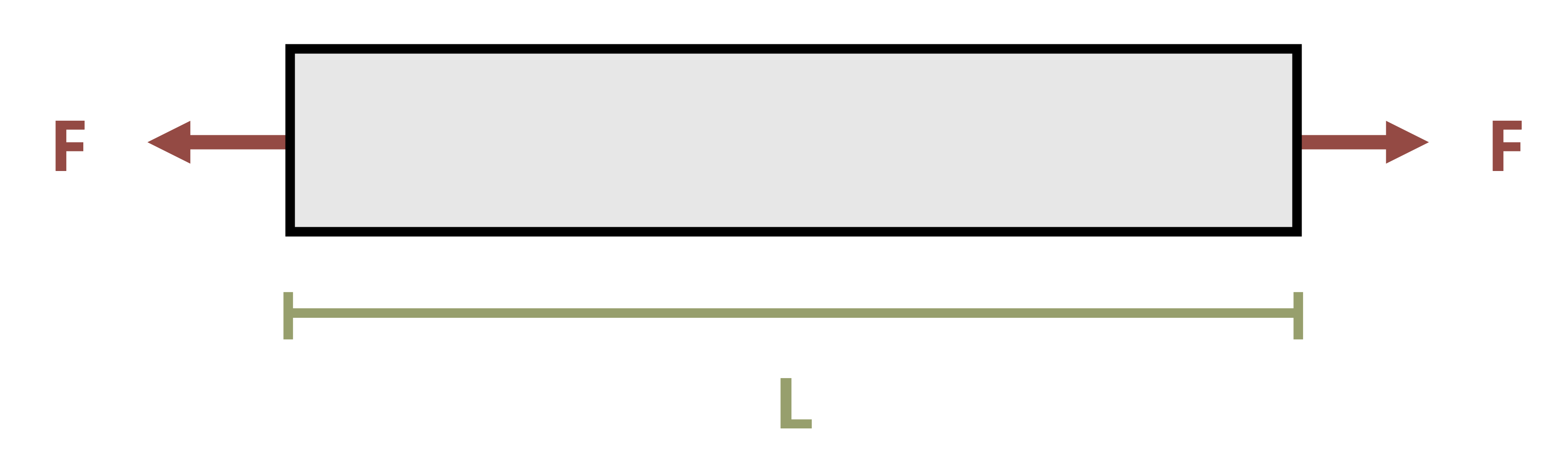
Assuming elastic behavior, we have equations for stress and strain, as well as Hooke’s law which relates the two equations:
\[ \begin{aligned} & \sigma=\frac{F}{A} \\ & \varepsilon_{long}=\frac{\Delta L}{L} \\ & \sigma=E \varepsilon_{long}\end{aligned} \]
Replacing the stress and strain terms in Hooke’s law:
\[ \frac{F}{A}=E \frac{\Delta L}{L} \]
Rearranging:
\[ \Delta L=\frac{F L}{A E} \]
This equation can be used to directly find the change in length of an object subjected to an axial load.
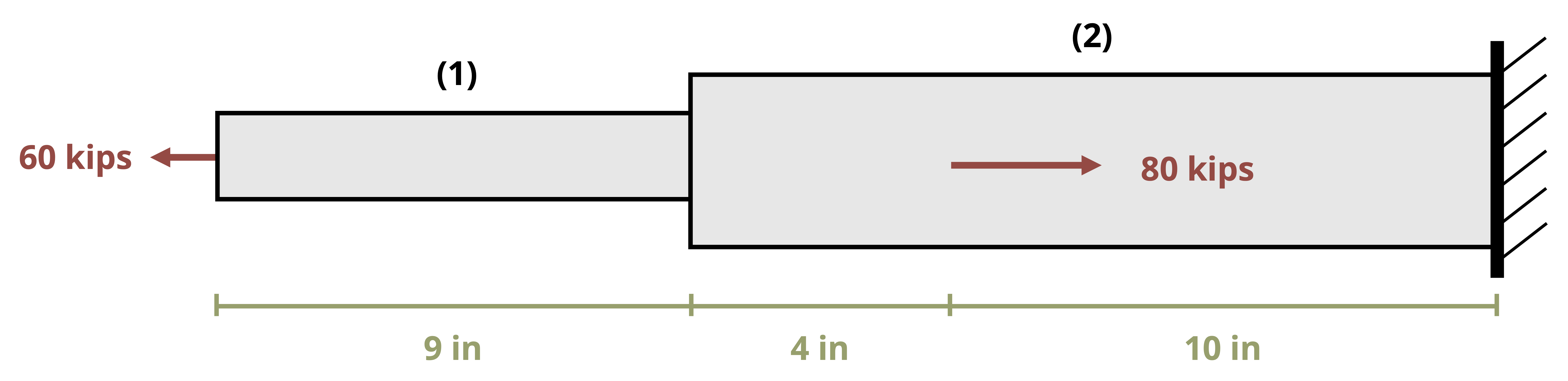
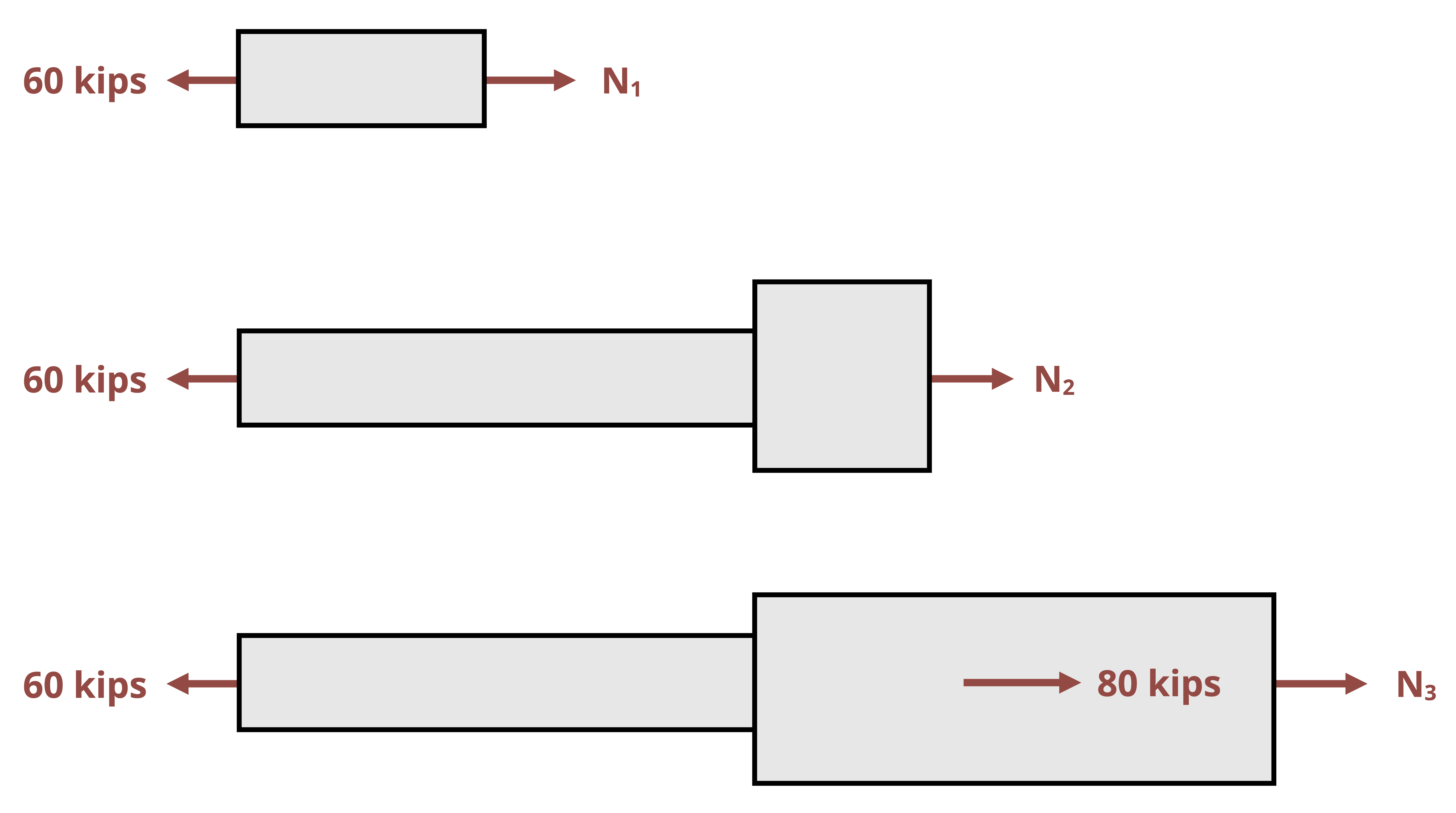
In practice, there may be multiple axial loads applied to the bar. The cross-sectional area may change at different points along the bar, or perhaps there could be different materials with different elastic moduli connected in series to form the bar. In any of these cases we can split the bar into sections where each section has a constant F, A, and E. We can calculate the change in length of each section separately and sum them to find the total. See Example 5.3 for a problem involving multiple segments of a bar.
\[ \boxed{\Delta L=\sum \frac{F L}{A E}} \tag{5.2}\]
ΔL = Change in length [m, in.]
F = internal axial load [N, lb]
L = Original length [m, in.]$
A = Cross-sectional area [m2, in.2]
E = Elastic modulus [Pa, psi]
5.4 Deformation in Series of Bars
Click to expand
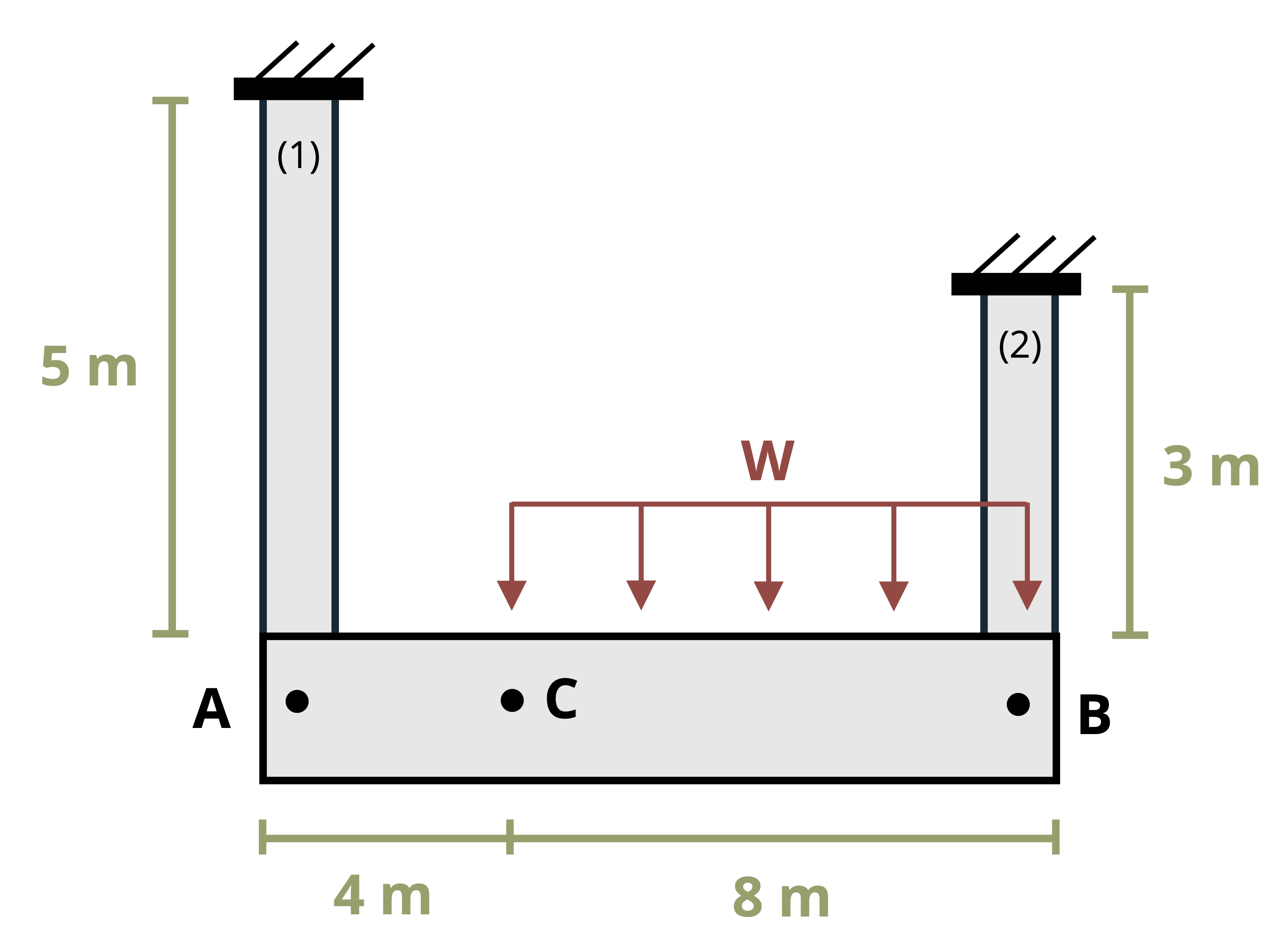
Sometimes a structure will have more than one axially loaded member. In such cases there are multiple bars that will experience a change in length and the amount of deformation won’t necessarily be the same in each member. The deformable members are generally connected by a rigid (nondeformable) beam. These problems generally involve a little geometry alongside our deformation equation (Figure 5.7).
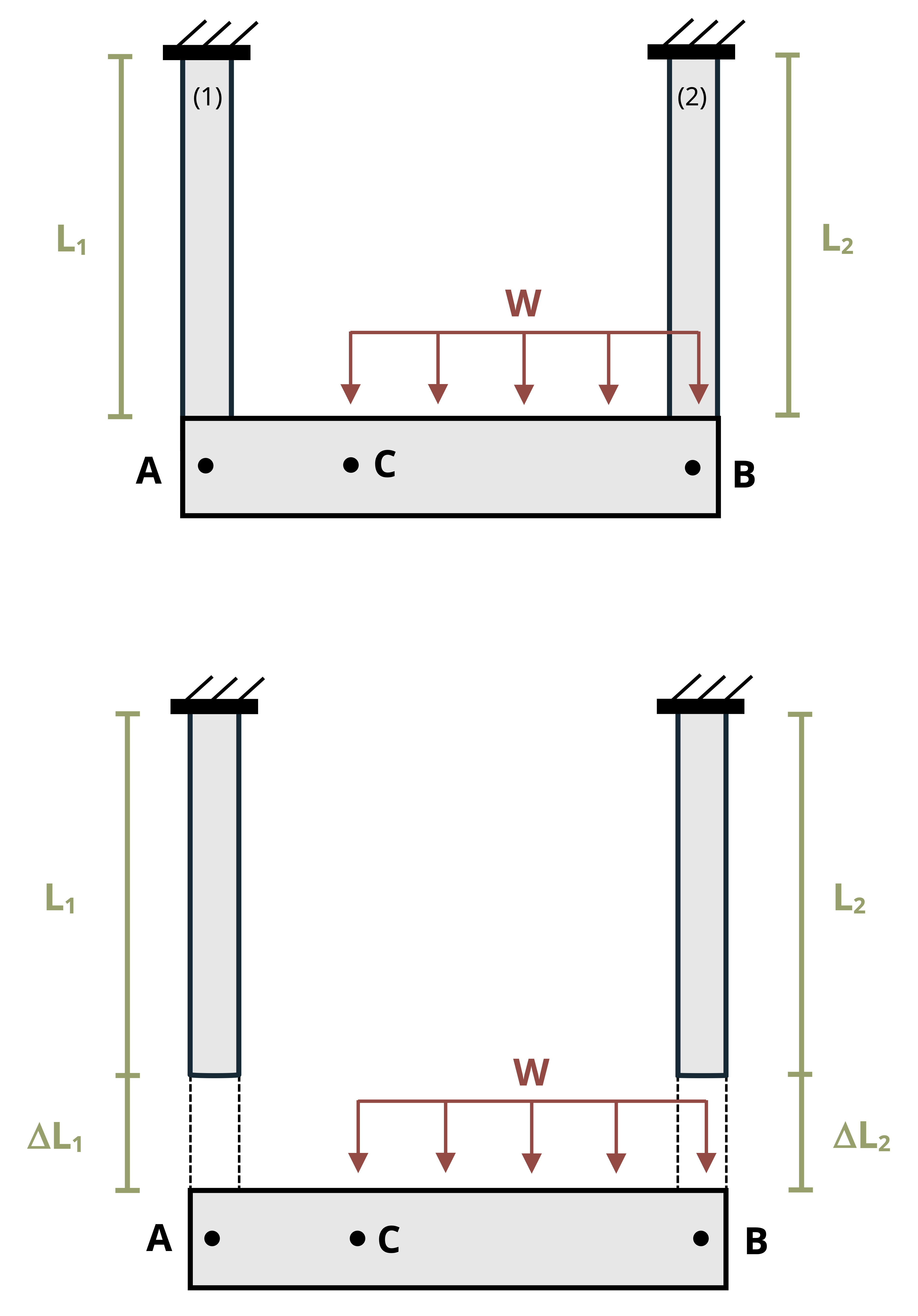
By identifying the force in each member through equilibrium, we may calculate the deformation of each member separately using:
\[ \Delta L=\frac{F L}{A E} \]
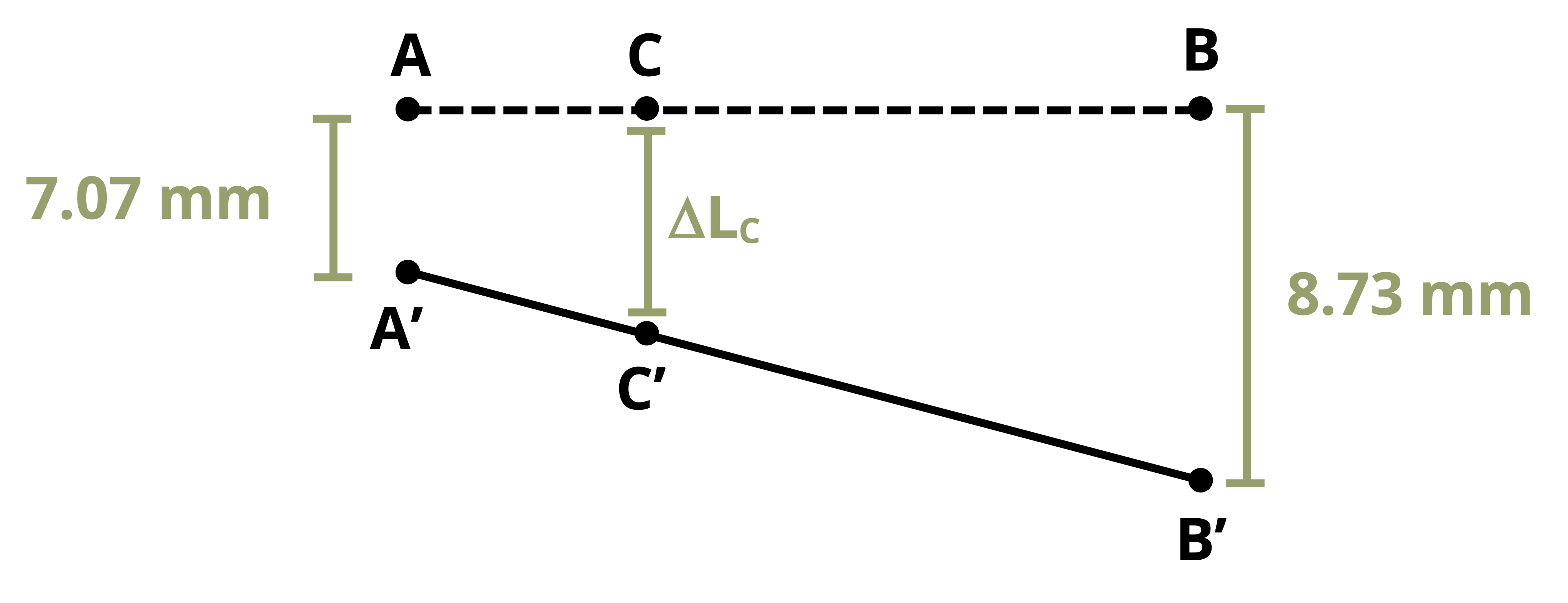
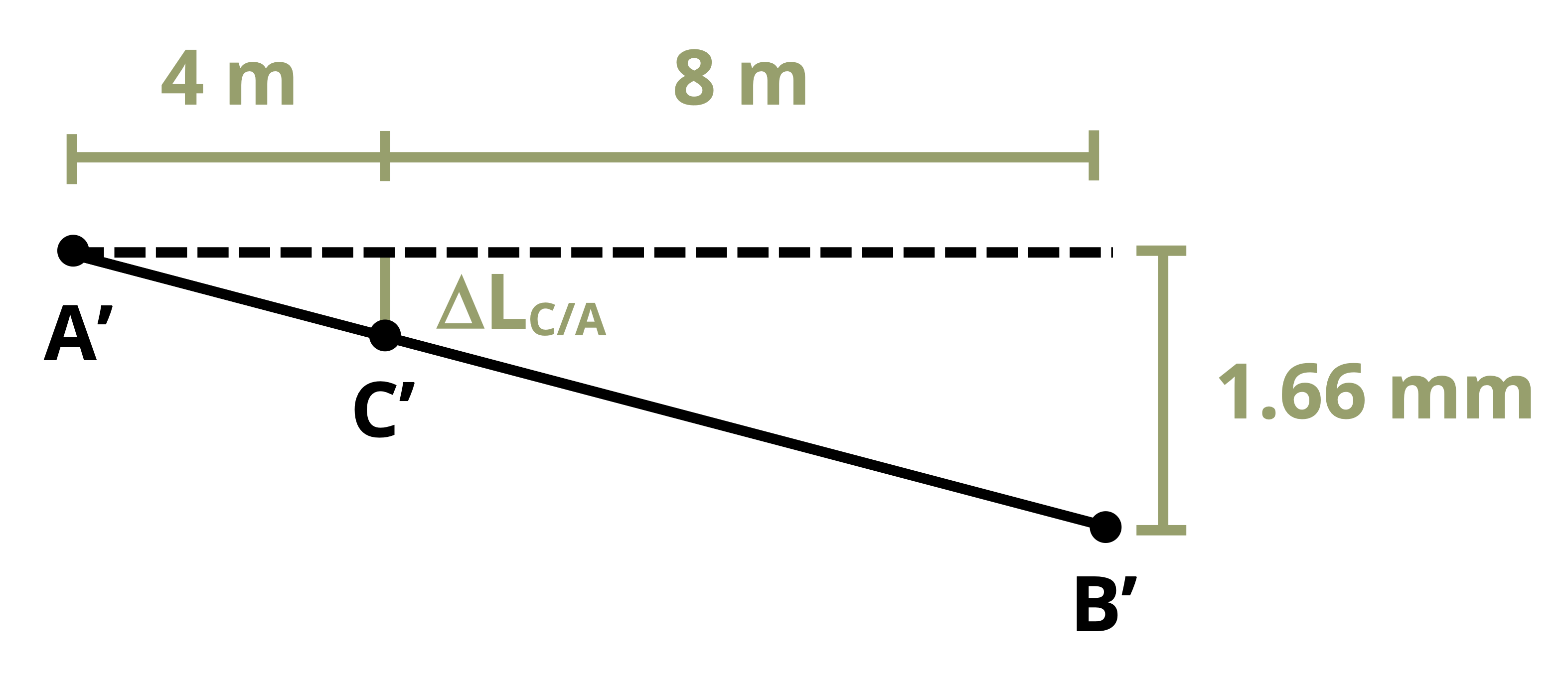
Once the change in length of each member is known, we can find the displacement at different points on the rigid beam through simple geometry of the rigid beam (Figure 5.8). This process is demonstrated in Example 5.4.
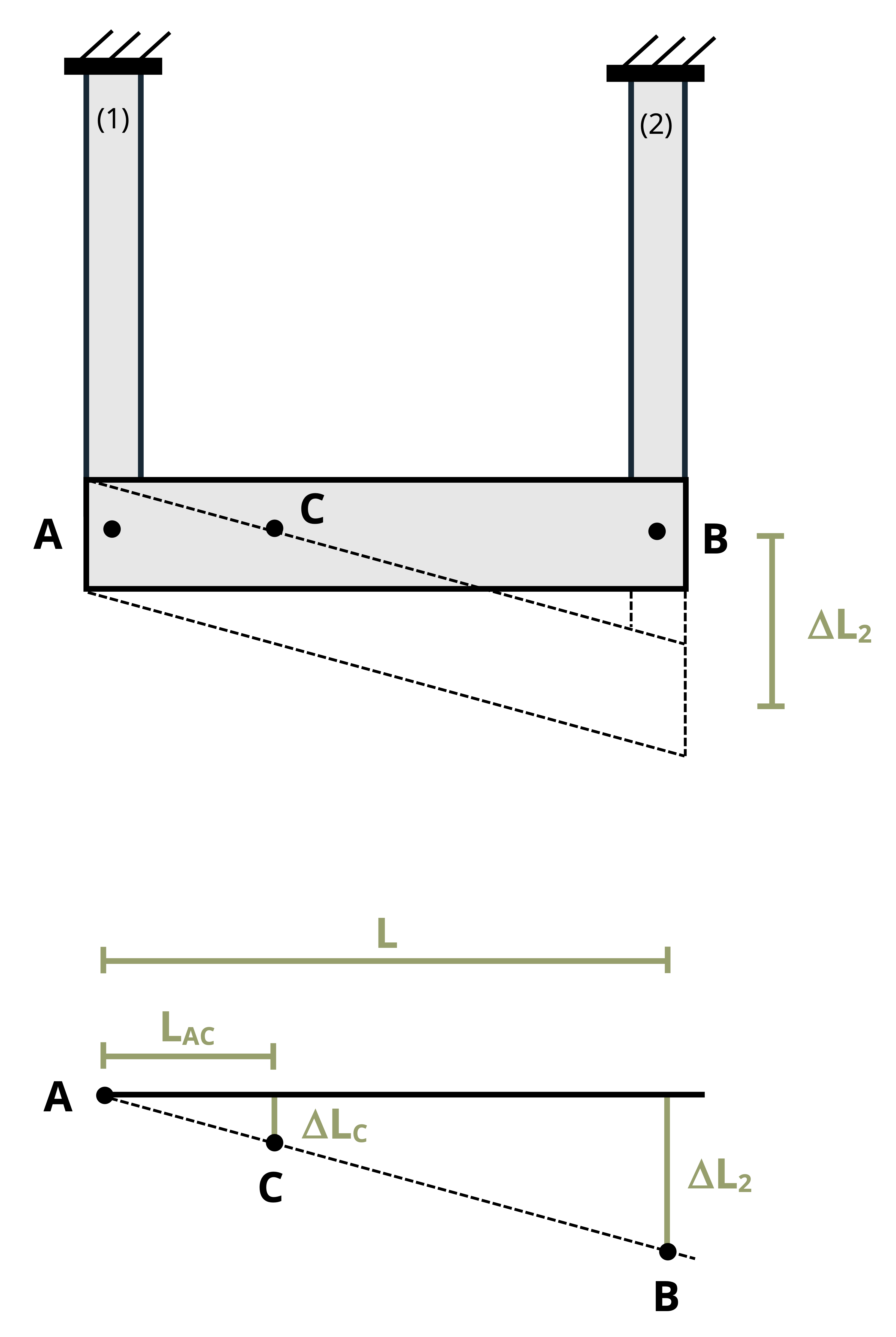
The deflection of point C will be somewhere between the deflection at A and the deflection at B. Assuming there is no deflection at A and assuming that the deflections (and therefore the angle at A) are small, we can use similar triangles to find:
\[ \frac{\Delta L_C}{L_{A C}}=\frac{\Delta L_2}{L} \rightarrow \Delta L_C=\Delta L_2 \frac{L_{A C}}{L}\]
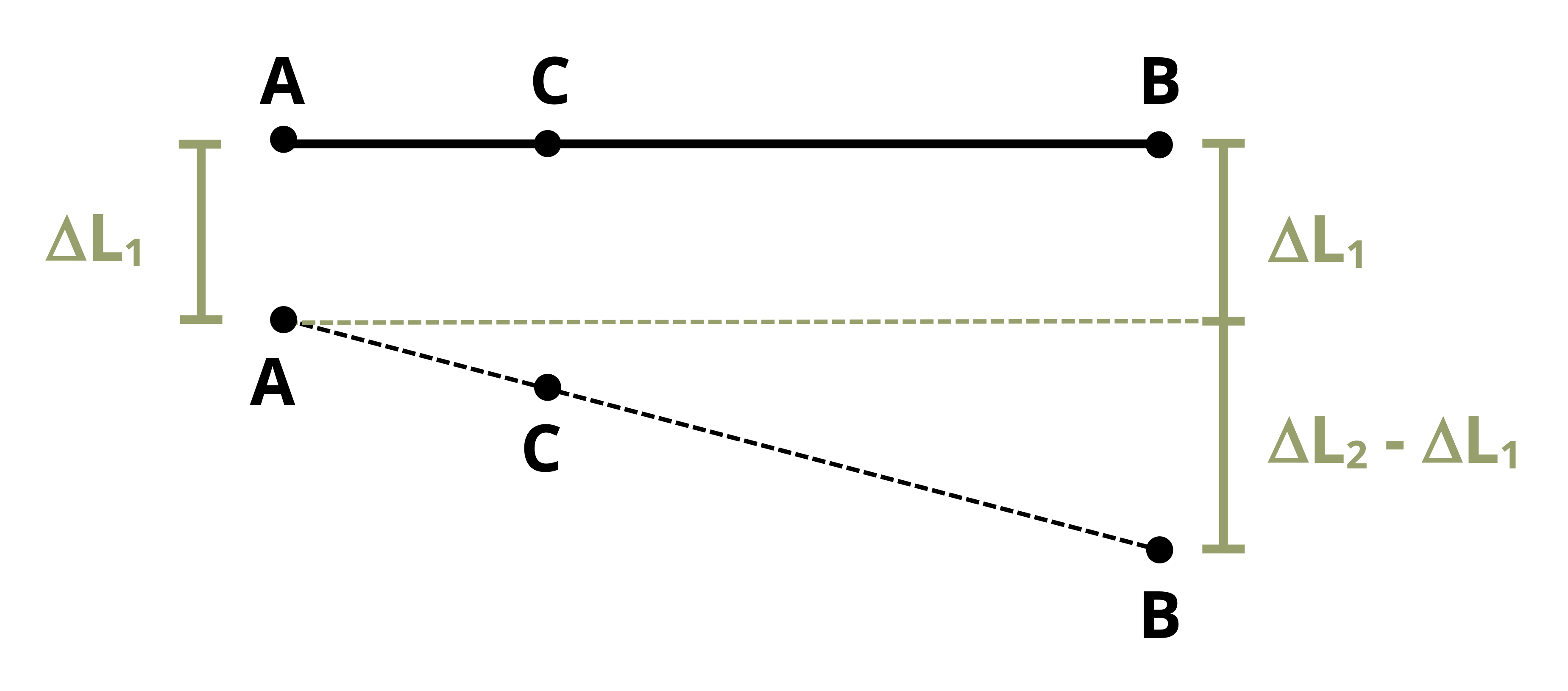
If there is a deflection at point A (Figure 5.9) this simply becomes:
\[ \Delta L_C=\Delta L_1+\left(\Delta L_2-\Delta L_1\right) \frac{L_{A C}}{L}\]
5.5 Statically Indeterminate Problems
Click to expand
A statically indeterminate problem is one which has more unknowns than we have equilibrium equations to solve for those unknowns. This is an issue because it prevents us from finding the internal loads and we therefore can’t calculate stress or deformation.
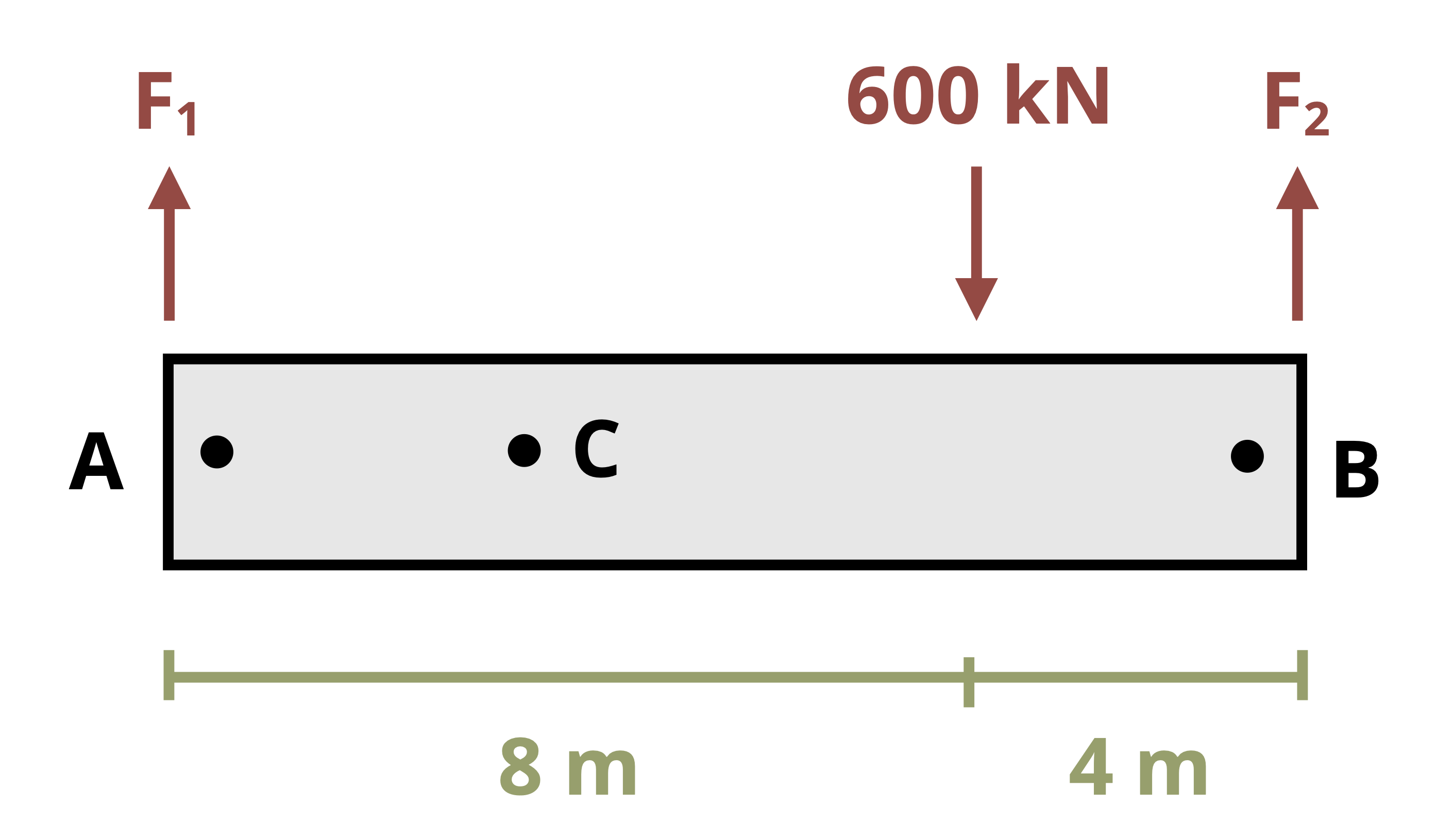
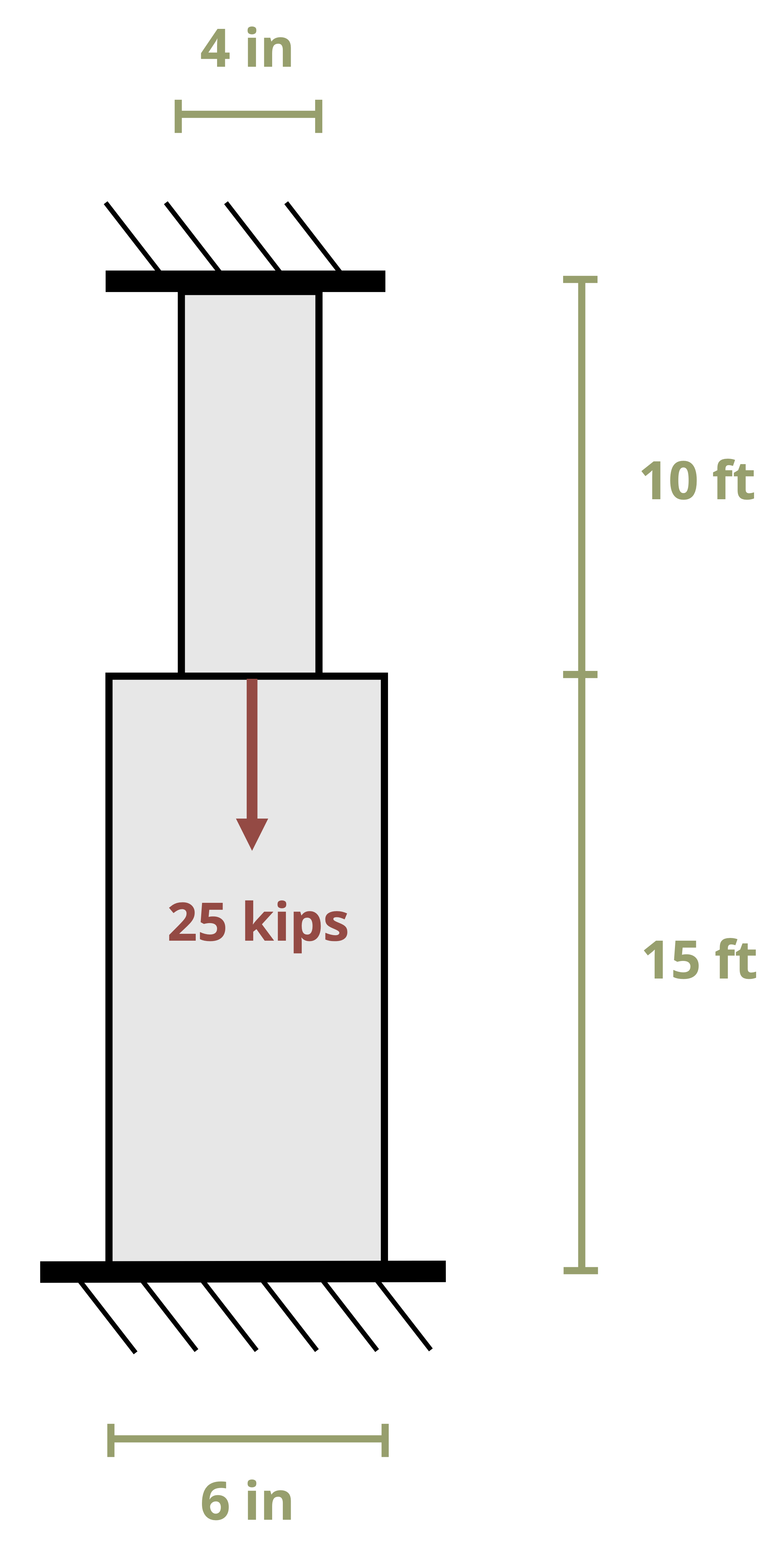
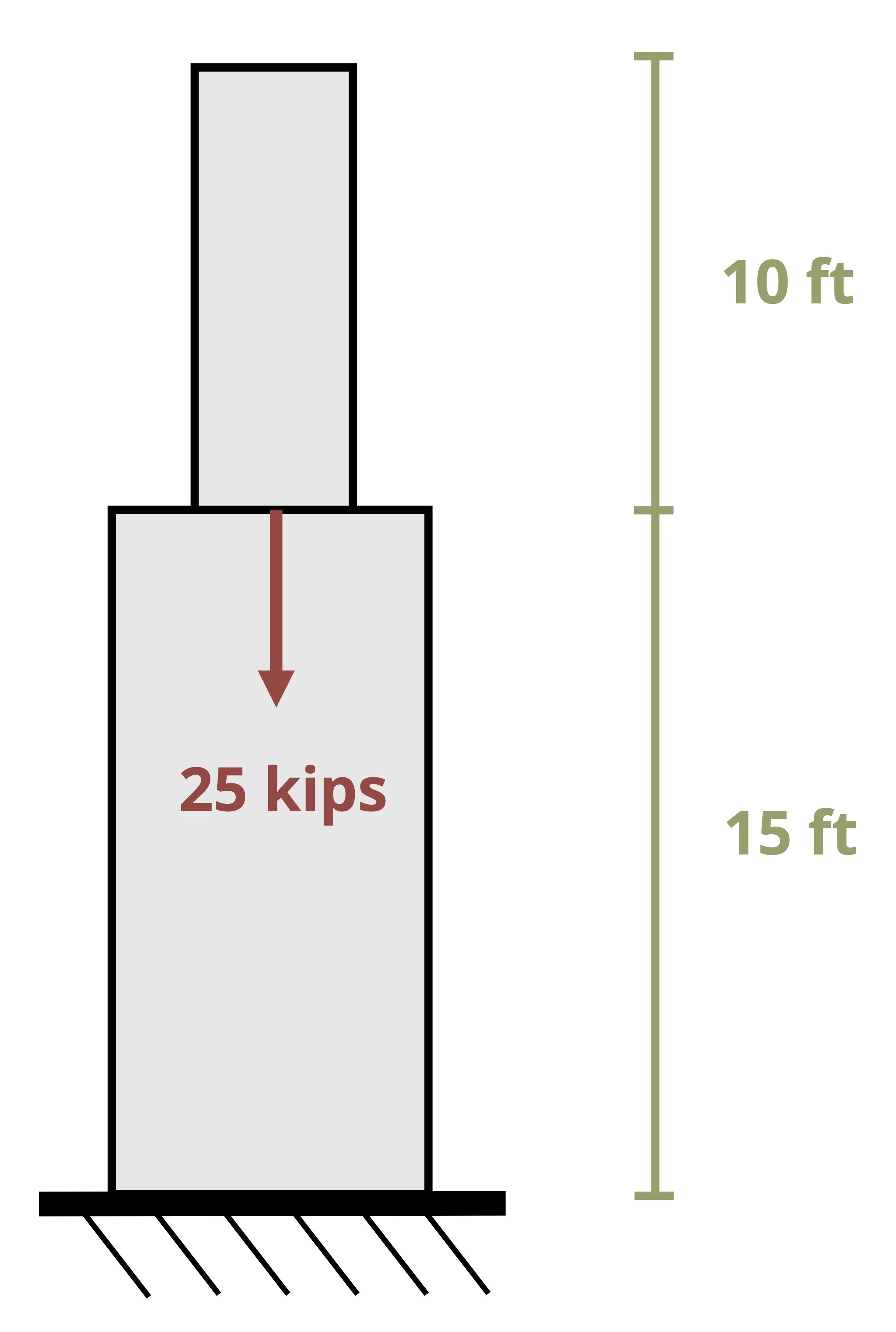
We’ll study two types of statically indeterminate problems. In the first type there will be additional supports beyond those needed to maintain equilibrium. These are known as redundant supports and they are quite common in practice (Figure 5.10).

In such problems, it is not possible to determine all of the reaction forces using equilibrium alone. However, we can use our knowledge of deformation to help. If a member is held between two supports then its total deformation must be zero. Since the change in length depends on the internal force in the member, this introduces an additional equation to use alongside the equilibrium equations. There are two possible approaches here.
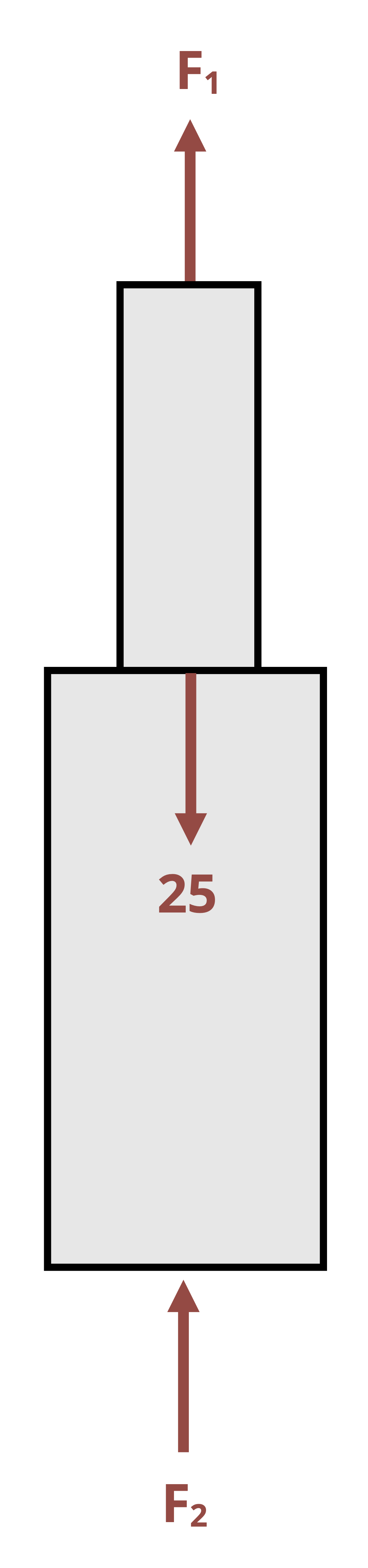
Approach 1: To determine the reaction force at the redundant support, begin by removing the redundant support from the problem and determining the deformation that would occur if the support was not there. Then replace the reaction force at the support, which will cause the member to deform in the opposite direction (Figure 5.11).
The sum of these two deformations must equal the actual deformation of the member. If the member is held between two rigid supports, the total deformation will be zero. If there is a small gap or the supports allow a certain amount of movement, the total deformation will be equal to the size of this gap. Example 5.5 shows this process applied to a bar made of 2 materials.
Approach 2: An alternate approach is to start by noting that the total deformation of the bar must be zero. In the case shown in Figure 5.12, we can say that the deformation of segment 1 plus the deformation of segment 2 must add up to zero.

The internal load in segment 1 is FA and the internal load in segment 2 is FB, so there are currently two unknowns. We may use an equilibrium equation to solve for these two unknowns simultaneously.
\[ \begin{aligned} & \frac{F_A L_1}{A_1 E_1}+\frac{F_B L_2}{A_2 E_2}=0 \\ \\ & F-F_A-F_B=0\end{aligned} \]
Example 5.6 re-solves Example 5.5 using this method instead.
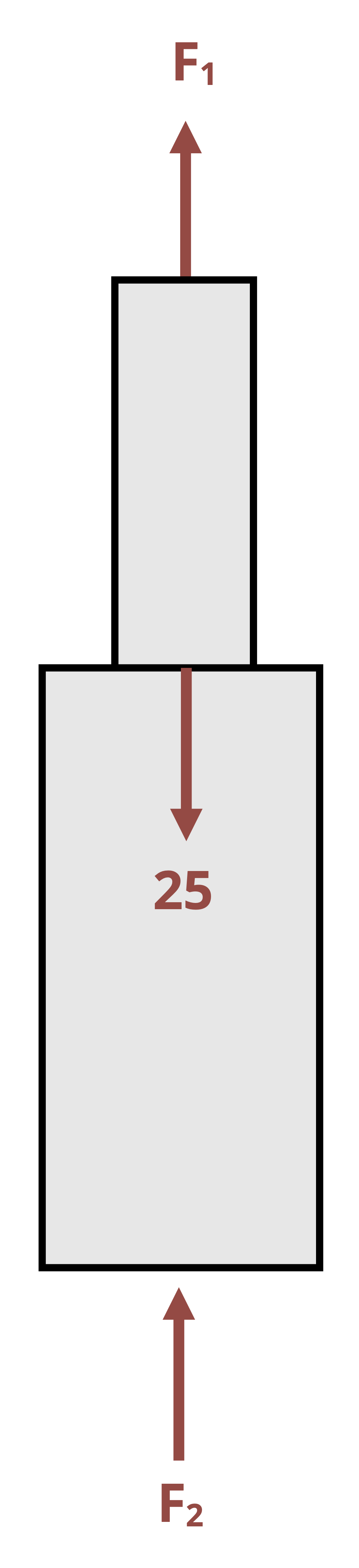
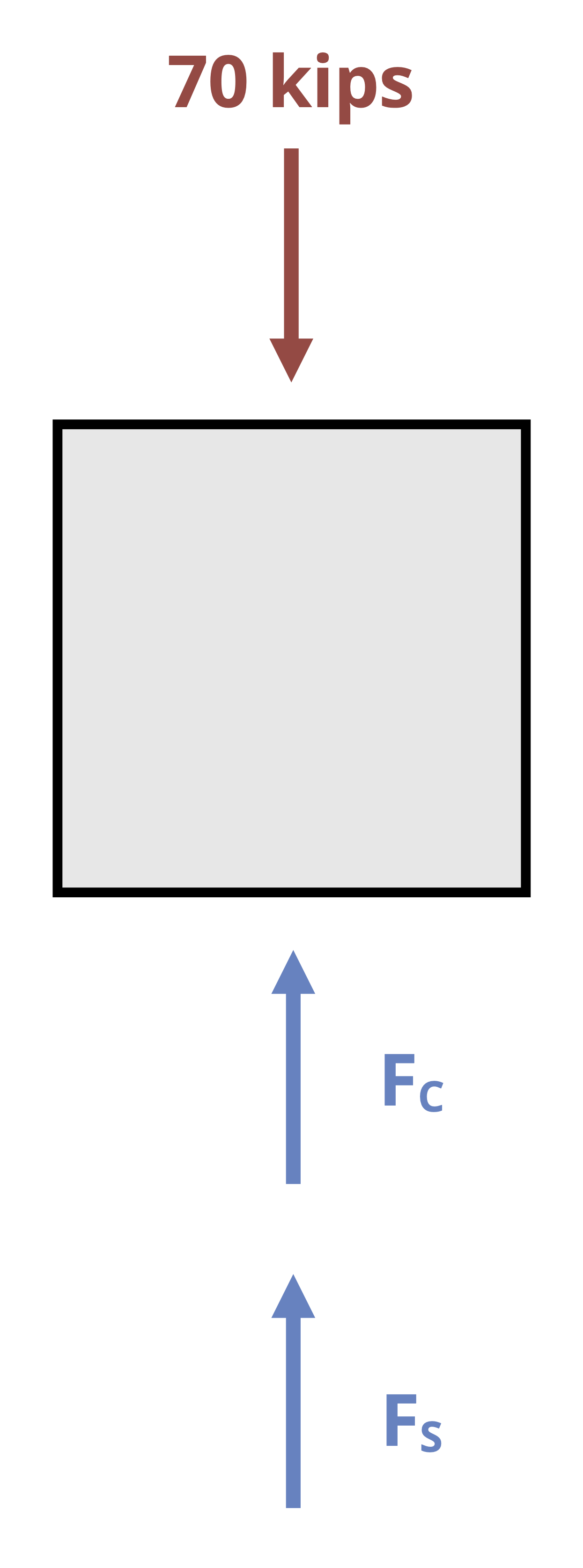
The second type of indeterminate problem involves two materials bonded together in parallel. In these problems it’s possible to find the reactions at the supports, but not possible to find the internal force in each material using only equilibrium (Figure 5.13).
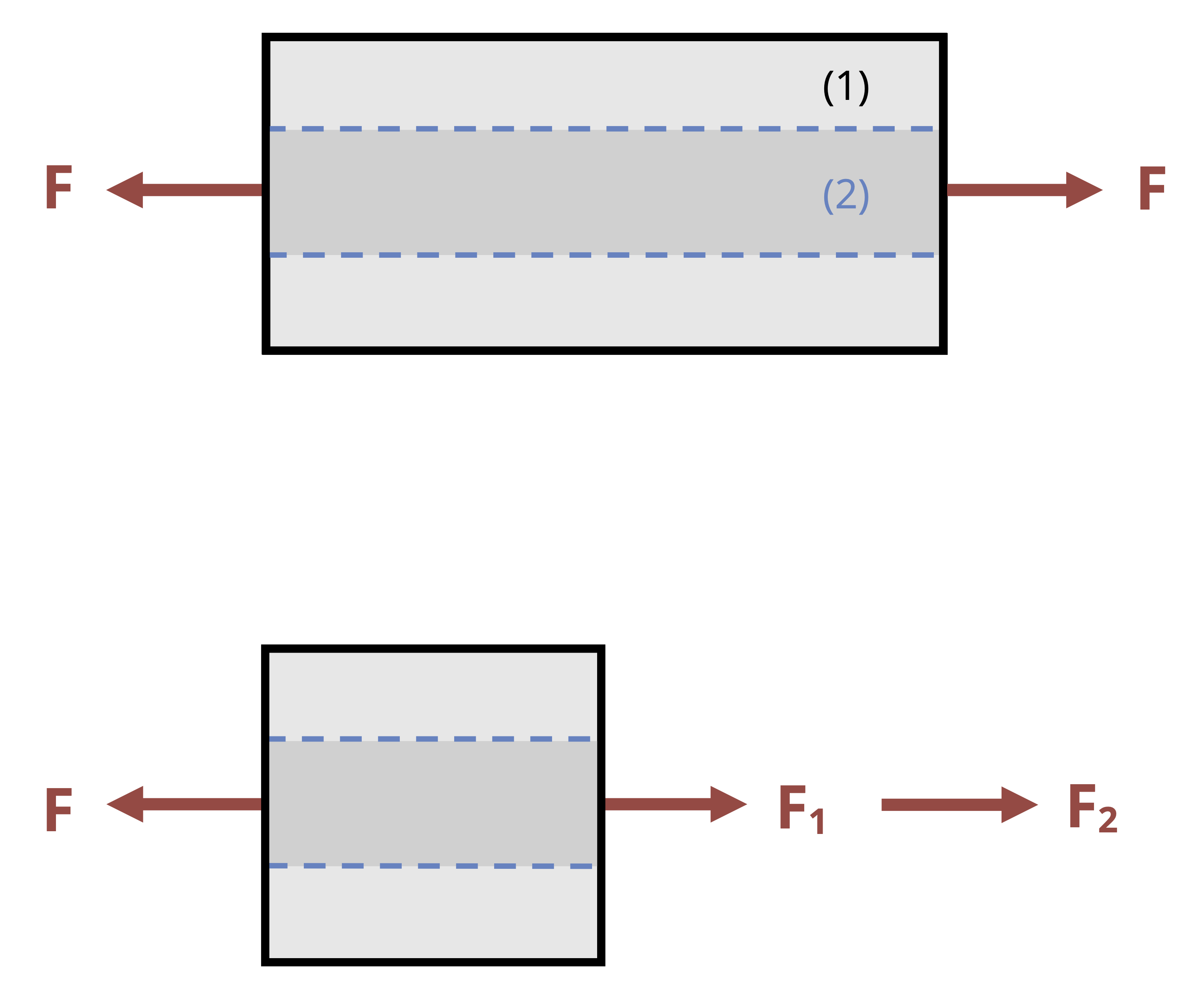
We have one equilibrium equation but two unknown internal forces. However, since the materials are bonded together we can say that they must deform by the same amount. By setting the deformation for each material equal to each other we can define a second equation that involves the two internal forces and, combined with the equilibrium equation, we can now solve for both internal forces. See Example 5.7 for a demonstration.
5.6 Thermal Deformation
Click to expand
So far, we’ve studied the effects of axial forces on an object and how they create stresses and deformations. Temperature changes will also cause an object to deform. As seen in Section 4.6, the strain due to temperature can be predicted by:
\[ \varepsilon_T=\alpha \Delta T \]
As before, strain is dimensionless. The coefficient of thermal expansion is a material constant that can be looked up in handbooks or in Appendix C. Note that for a given change in temperature, the thermal strain will be the same in the axial and transverse directions.
Since strain is also defined as \(\varepsilon=\frac{\Delta L}{L}\), we can also predict the deformation due to a change in temperature:
\[ \varepsilon_T=\alpha \Delta T=\frac{\Delta L}{L} \quad\rightarrow\quad \Delta L=\alpha \Delta T L \]
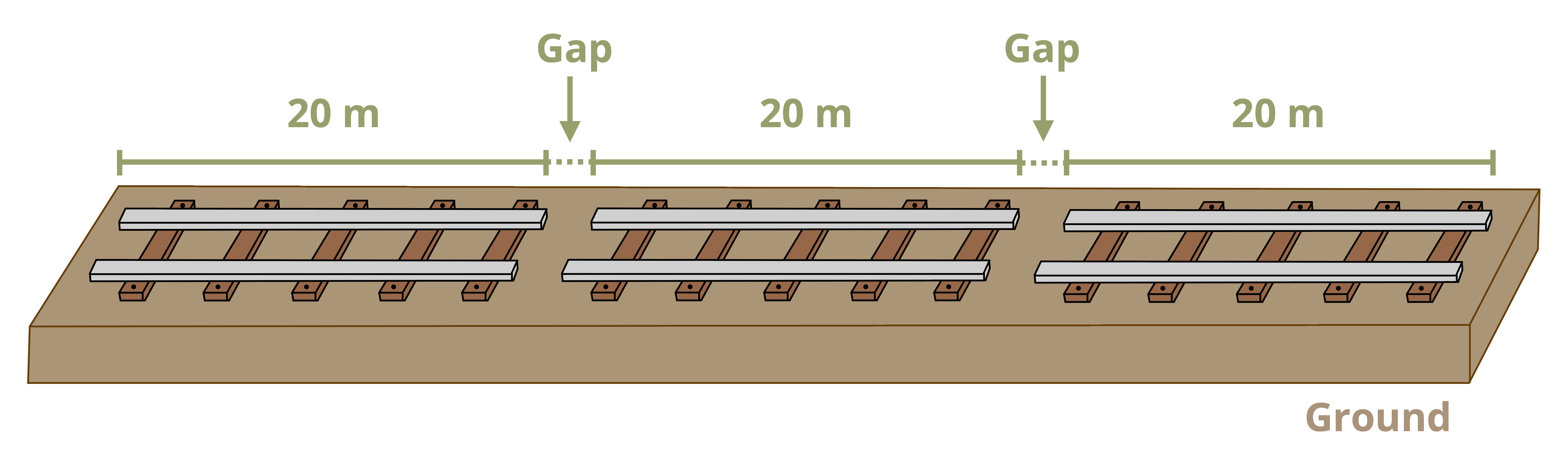
If the object is free to expand or contract this doesn’t cause any issues and is easy to account for. Many real applications will include a small gap to allow for changes in length due to temperature changes (Figure 5.14). It is even possible that an object is subjected to both a physical force and a temperature change and the total change in length is simply the sum of these effects:
\[ \boxed{\Delta L=\Delta L_F+\Delta L_T=\frac{F L}{A E}+\alpha \Delta T L} \tag{5.3}\]
𝛥L = Change in length [m, in.]
𝛥LF = Change in length due to applied load [m, in.]
𝛥LT = Change in length due to temperature change [m, in.]
F = Internal force [N, lb]
L = Original length [m, in.]
A = Original cross-sectional area [m2, in.2]
E = Elastic modulus [Pa, psi]
𝛼 = Coefficient of thermal expansion \(\left[\frac{1}{^\circ C}, \frac{1}{^\circ F}\right]\)
𝛥T = Change in temperature \([^\circ C, ^\circ F]\)

However if we do not design a gap, or if the gap is not large enough, then the object is not free to expand or contract. As the member pushes or pulls on its supports, a physical force is created. This in turn creates a stress in the object and these stresses can be very large. Such problems are statically indeterminate as the force applied on the member by the support is unknown and can’t be found using only equilibrium. Solving these problems is very similar to solving the first type of statically indeterminate problem. First, remove a support and determine the amount of deformation that would occur due to the change in temperature if the object were free to deform. Then replace the force from the removed support, which will cause the object to deform in the other direction. The sum of these two deformations will equal the total deformation of the member as before. Example 5.8 works through an indeterminate thermal expansion problem.